Závěrečné fórum - opět individuální

Matematika v ekonomii mi zabral ve srovnání s ostatními předměty při vypracování úkolů velkou část mého času, avšak na druhou stranu jsem se připravovala na předmět průběžně a ne nárazem. Svou práci si mohu v této fázi strukturovaně zobrazit na svém blogu (moje studijní portofolio). Průběžné práci jsem věnovala průměrně na každé vypracování úkolu přibližně dvě hodiny, jak i kolegyně v týmu. Tvrdá práce, časová náročnost a samostatné studium látky v konečné fázi přinesla při SPP očekávaný výsledek. 

Dynamické modelování

Další z týmových fór.

1. Dynamické modelování v mikroekonomii:

A Procvičte si teorii na příkladech (s obrázky!)
- stačí pro nespojité změny
- se zpožděním na obou stranách
- pokaždé vedoucí ke konvergenci, resp. divergenci, celkem příklady.

B Látku si shrněte ve STRUKTUROVANÉM PŘEHLEDU - pro Vaše snadnější pochopení a zapamatování zákonitostí konvergence.

2. Dynamické modelování v makroekonomii - stačí jeden příklad s obrázkem.

Funkce dvou proměnných slouží ekonomii - teorie užitku, teorie firmy, teorie investičního rozhodování

Jedno ze tří týmových fór

A Procvičení na příkladu teorie užitku

B Využití matematické abstrakce pro přechod od jednoho modelu k druhému - SYSTEMIZACE!

Tato část úkolu musí být bezpodmínečně zpracována velmi kvalitně. Vytvářejte k sobě příslušné položky, např. do tabulky - viz přednáška a cvičení. Nezapomeňte na grafická srovnání.

Extrémní účinky fiskální a monetární politiky

Vypracujte si přehled extrémních účinků politik. Vždy řešte účinek pomocí limity.

Velikost vytěsněné produkce vlivem fiskální, resp. monetární politiky

Modelujte velikost vytěsněné produkce - početně a graficky. Tam, kde je to možné použijte obě metody výpočtu (1. pomocí bodů, 2. pomocí multiplikátorů), a tam, kde to možné není, použijte pouze metodu možnou.

• vlivem fiskální politiky
1. podoba fisk. pol.
2. podoba fisk. pol.
• vlivem monetární politiky

Každý student JEDEN příklad na fiskální politiku a JEDEN příklad na politiku monetární. Každý student bude mít příklad s vlastní volbou hodnot, tzn. každý příklad bude JINÝ. Pro KONTROLU Vám slouží co nejpřesněji nakreslený GRAF znázorňující zvolenou INTERVENCI.

Výpočet vytěsnění pomocí bodů a multiplikátorů mi nevyšel shodně. Nevím, buď je chyba někde v průběhu výpočtu a nebo nahozením čísel...

Obrázky jsou v náhledu méně čitelné, pro čitelnější rozlišení je dobré si to stáhnout jako obrázek.

POZOR!!! Sklony IS, LM pro konkrétní změny citlivostí

Procvičujte příklady ze skript (elektronický text v repository) kapitola IS-LM, ale volte své vlastní zadání, tj. jiná čásla než jsou ve skriptech a než jsme řešili ve cvičeních!

KAŽDÝ STUDENT ALESPOŇ JEDEN Z NÁSLEDUJÍCÍCH 5 PŘÍKLADŮ - vždy početně i graficky, pokaždé odvozením přes AD, resp. L, ale také přímo z rovnic IS, resp. LM):

Každý odevzdaný příklad musí mít 4 části - pro přehlednost označte A, B, C, D - navzájem musí souhlasit, tj. nikdo nemůže mít chybný výsledek :-):

1. A Analytické odvození křivek z různými sklony + popis toho, co se stalo a čím to bylo zapřičiněno
2. B Grafické odvození křivek z různými sklony + popis toho, co se stalo a čím to bylo zapřičiněno + kontrola s předchozím
3. C Analytické vyjádření křivek s pouitím vzorců  + popis toho, co se stalo a čím to bylo zapřičiněno + kontrola s předchozím
4. D Grafické zakreslení výsledků z bodu C  + popis toho, co se stalo a čím to bylo zapřičiněno + kontrola s předchozím

Své příspěvky ve fórech TŘIĎTE do 4, resp. 5 skupin!

Řeště příklady s jinými čísly, než jsou ve skriptech nebo byla zvolena na cvičeních, tj. počítejte svůj příklad! ==> každý příklad bude jiný ( a od každého tam bude - aspoň jeden se 4 částmi :-) !)

1. úkol 2 ze skript: změna alfa (? sklon IS, multiplikační účinky) - volte změnu c
2. úkol 2 ze skript: změna alfa (? sklon IS, multiplikační účinky) - volte změnu t
3. úkol 3 ze skript: změna b (? sklon IS, multiplikační účinky)
4. úkol 5 ze skript: změna k (? sklon LM, multiplikační účinky)
5. úkol 5 ze skript: změna h (? sklon LM, multiplikační účinky)

Přehledně zapsat, přehledně zakreslit!!!

Nechť je četnost všech 4 příkladů srovnatelná, tj. dělej to, co je dosud ve fóru nejméně!

Sklony a posuny křivek IS, LM

Které veličiny ovlivní sklon, resp. posun křivky IS, resp. LM. Snažte se formulovat ekonomickou situaci, tu převeďte do mluvy lineárního modelu. Všechno kreslete, popisujte, zdůvodňujte. 

Modelovat můžete také polohy funkcí poptávky pro změny zafixování tzv. "cizích" veličin (AD pro různá i, resp. L pro různá Y).

Akumulace kapitálu

Jak jsem si procvičil akumulaci kapitálu. Zejména v obrázcích zdůrazněte vztah mezi derivací a určitým integrálem - všechno viz animovaný výklad (repository).

A početní příkladek: 

Makroekonomická rovnováha ve třísektorové ekonomice; multiplikační efekt (efekt změny autonomních výdajů, resp. mpc, resp. t)

Odvoďte multiplikační efekt ve tří sektorové ekonomice (případně s konkrétními čísly). Postupně můžete nejen "stavět nemocnici", ale také měnit velikost transferů, resp. autonomních daní, ba dokonce daňovou sazbu. Kdy se AD pouze posunuje, kdy se dokonce otáčí?

Multiplikační efekt vyznačte graficky.

DOPLNĚNÍ ÚKOLU (každý nechť má zápisky a hl. obrázky ke každé z těchto situací!): Analyzujte multiplikační efekty pro

1. změnu některých z autonomních výdajů (1-3 sektorová ekonomika)
2. změna mpc (zvýší se multiplikační efekt nebo sníží, proč?)
3. změna t (zvýší se multiplikační efekt nebo sníží, proč?)

Každou ze zakreslených situací si napište symbolicky (jako informaci, kterou stojí za to si zapamatovat), např. zvýšení mpc znamená strmější spotřební funkci, tzn. průsečíky pro rovnováhu jsou dále od sebe, tj. multiplikační efekt na důchod se pro větší mpc zesiluje - zapište v symbolech šipek, implikací atd.

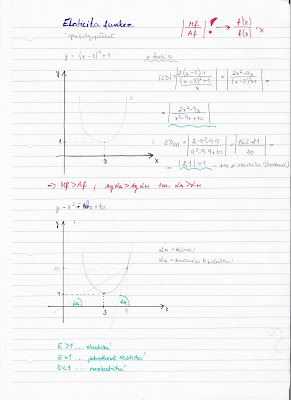
Elasticita, včetně paradoxu velké úrody atd.

Příklady k postupnému procvičování

• Zvol funkci rostoucí, resp. klesající a urči graficky jejich elasticity (viz přednáškové slidy).
• Zvol funkci nabídky (kvadratickou) a urči její elasticitu jako funkci, pak v jednom bodě - početně, graficky (viz příklad ze cvičení).
• Skupinový příklad pro změny diskrétní (pro poslední dodatečnou jednotku, viz Vaše ekonomické příklady, např. o snižování cen letenek apod.) - jen pro zájemce (nemusíte).
• Paradox velké úrody, resp. snížení poplatků za telefon (velmi často bývá na písemkách)!!!

Fórum: vztah funkcí mezní a průměrné

Kreslete sady obrázků Mf a Af a žádejte po svých kolezích ve skupince í výběr správné odpovědi - viz přednáška (začněte někdo upřesněním zadání, jak jste jej slyšeli, např. komentováním svého zadání a správného řešení).

Který z obrázků je správně?

Vztah mezi veličinami průměrnými a mezními - zadání v ppt. prezentaci

Řešte úkol z přednášky. Začněte někdo tím, že připíšete zadání, jak jste jej dostali z prezentace na přednášce.




A já už pokračuji jen úkolem...

Pozn. v druhém grafu, při kreslení čáry špatně vyšel odhad a minimum průměrných nákladů neprotíná množství 6, jak by správně měly ve svém minimu! 

Maximalizace zisku

Výpočtem hledejte maximální zisk pomocí dvou metod:

1. MC = MR (ekonomické pravidlo)
2. Hledání extrému funkce (využití diferenciálního počtu)

a hledejte spojitosti obou výpočtů.

Zakreslete pod sebe 3 související grafy a do nich VŠECHNY RELEVANTNÍ ÚDAJE A SOUVISLOSTI (POPIŠTE CO NEJVÍCE):

1. TR, TC
2. MR, MC
3. zisk pi

Hledejte pro funkce:

• TR = 11 300 Q - 22Q²
• TC = 4 Q³ - 16 Q² + 140 Q + 1780

Pro nákresy určujte vrcholy, resp. konvexnost a konkávnost funkcí aj.

Hladká funkce

"Křivka ekonomická je hladká (v bodě, resp. v intervalu) tehdy a jen tehdy, má-li spojitou derivaci."  

Inspirace -  studijní materiál z Repository s názvem Hladká funkce. 

Příklad ze 4.cvičení:

Mezní sklon ke spotřebě (marginal propensity to consume, MPC)

Mezní sklon ke spotřebě říká praktickou odpověď na otázku „jaký máme sklon spotřebovávat“. Limity nám pomáhají určovat hodnoty tam, kam ve skutečnosti nedosáhneme, např. v nekonečnu či k nule.

Ve dvousektorové ekonomice existují jen domácnosti a firmy, tzn. nepřichází v úvahu žádné sociální dávky a pokud není možno spotřebovávat z důchodu, jedinou další možností je čerpat z úspor!

Důchod Y je nezávisle proměnná a spotřeba C je závisle proměnná. Funkce f vyjadřuje vztah, který mezi proměnnými existuje. C = f (Y), tzn. y = f (x) "Spotřeba je funkcí důchodu“. Situace v bodě A [0, 0] znamená, že pro nulový důchod je i spotřeba nulová (SPOTŘEBNÍ FUNKCE JE ROSTOUCÍ).

Při nulové spotřebě musí být spotřeba kladná. 

Autonomní spotřeba vyjadřuje hodnotu spotřeby nezbytně nutnou, tj. takovou, která musí být spotřebována, i když je důchod nulový.

Spotřební funkce NENÍ LINEÁRNÍ: Rovnovážný bod (jeden bod celé spotřební funkce je takový, že poskytovaný důchod a jeho spotřeba jsou v rovnováze, tzn. PRŮSEČÍK spotřební funkce s osou kvadrantu C = Y.  Pro stále stejné přírůstky Dx (u nás je to DY – přírůstek důchodu, protože nezávisle proměnnou je důchod) jsou přírůstky Dy (pro spotřební funkci DC – přírůstek spotřeby, protože závisle proměnnou je spotřeba) menší a menší. Čím je člověk bohatší, utrácí menší procento svého dodatečného příjmu. Důchod klesá od 1 až k 0 pro hladkou spotřební funkci obrázek č. 2 první řádek vpravo.
Spotřební funkce je rostoucí, její derivace (rychlost) je však klesající.

„C₀“ je autonomní spotřeba. „c“ označuje mezní sklon ke spotřebě – v ekonomii.
Funkce MPC klesá degresivně - "Je-li Větší než nula, je funkce konVexní a naopak". Klesá neomezeně až do nekonečna. Funkce MPC neklesá neomezeně, ale její dolní hranicí je funkční hodnota nula.
MPC je klesající. MPC klesá od hodnoty 1 k hodnotě nula pro rostoucí hodnoty nezávisle proměnné. MPC je KONVEXNÍ. 

Také je v tomto grafu znázorněna obecně zapsaná posunutá logaritmická křivka. Její průběh odpovídá ekonomickým zákonitostem pro spotřební funkci. C: C = ln (Y + 1) + c,   Y >0   (důchod je vždy kladný). 

LINEÁRNÍ funkce je matematicky vyjádřena jako y = k . x + q, kde k je směrnice přímky, (derivace) neboli její SKLON (c je totéž jako k; C₀ je totéž jako q). „C₀“ je autonomní spotřeba. „c“ označuje MEZNÍ SKLON KE SPOTŘEBĚ – v ekonomii. DERIVACE (naší) spotřební funkce, tj. mezní sklon ke spotřebě je dán vztahem: C = c + mpc * Y 

Přímka Y = C je osou kvadrantu (pokud je měřítko na osách shodné). Nezávisle proměnná se rovná závisle proměnné. 

Obrázek č. 4 rychlost tečen se nemění, úhel tenčen se taktéž nemění. Závisle a nezávisle proměnné jsou menší než 1 odpovídá hledanému úhlu tangens. 

ÚSPOROVÁ FUNKCE : S = Y – C; S: S = Y – [ln (Y + 1) + s],   Y >0   (důchod je vždy kladný). Viz. obrázek č. 5.. MEZNÍ SKLON K ÚSPORÁM a značí se MPS. MPS je  rostoucí,  konkávní,  její nejmenší hodnota je 0 a největší je 1.
Obrázek č. 6 zobrazuje chování funkce -  Mezní sklon k úsporám hovoří o chování funkce úsporové, jelikož je její derivací. Vidíme také na následujícím obrázku: je to hodnota 1. Tato jednička odpovídá tangens hledaného úhlu, ten je proto roven 45⁰.


Závěrem to chce shrnutí:

Funkce SPOTŘEBNÍ je rostoucí, konkávní. Její derivace – mezní sklon ke spotřebě – je klesající, a to od jedné k nule, a konvexní.

Funkce ÚSPOROVÁ je rostoucí, konvexní. Její derivace – mezní sklon k úsporám – je rostoucí, a to v intervalu od nuly k jedné, a konkávní.

Funkce a její derivace

Nakreslete pod sebe 3 související grafy (stejné měřítko na ose nezávisle proměnné). V prvním nakreslete zvolenou funkci, ve druhém její derivaci, ve třetím její druhou derivaci. Popište co nejvíce, co umíte z funkcí vyčíst, např. kdy (tj. pro které hodnoty nezávisle proměnné) je ta která funkce např. rostoucí a proč - ukažte, jak se projevuje na navazujícím grafu ...

"Derivace je silný nástroj, který popisuje chování ekonomické funkce v každém jejím bodě." 

Sklon funkce na intervalu a v bodě. Posun a otočení křívky. Extrém funkce a její derivace.

Jednou z možností je nakreslit pod sebe dva grafy (stejné měřítko na ose nezávisle proměnné). Do horního obrázku funkci (např. s extrémy, inflexními body apod.) a do spodního obrázku její derivaci. Pozor na souvislosti - zvýrazněte je, popište.

Různé funkce ze 4. cvičení:

Záměna os může být osudná

• Prolistujte svou ekonomickou knihu a najděte graf, ve kterém jsou nezávisle a závisle proměnná na opačných osách, než je v matematice obvyklé.
• Simulujte chybu, které byste se mohli záměnou dopustit.
• Pokud nenajdete nic jiného, zaměřte se na S-D model - nelineární! Pozor na "prohnutí" křivek - opticky je pokaždé jiné.

Podoba úkolu:

• Nakreslete lineární funkci do grafu s nezávisle proměnnou x na vodorovné ose. Zapište její předpis.
• Nakreslete funkci s tímtež předpisem do vedlejšího obrázku s osou nezávisle proměnné x na svislé ose.

Při sestavování grafů jsem se zaměřila na model nabídky - poptávky na konkurenční trh pohostinské činnosti. Na prvním grafu a) je zobrazen ekonomický pohled, na kterém je závislá proměnná počet zákazníků (osa x), kteří navštíví kavárnu a nezávislá proměnná cena kávy (osa y). Na grafu b) můžeme vidět matematický pohled, na kterém jsou osy přesně naopak. Množství zákazníků může kavárna ovlivnit stanovením výši své ceny za kávu na daném konkurenčním trhu. Z ekonomického pohledu je kavárna "price taker" a musí cenu přijmout. Pokud se podíváme na oba grafy vidíme, zcela rozdílné zobrazení.
Na obrázku a) má křivka nabídky (S) konvexní tvar s rychlejším trendem a na obrázku b) má křivka nabídky konkávní tvar s pomalejším trendem.  Křivka poptávky (D) zobrazuje velký počet zákazníků, lze usoudit. Také můžeme ve vyobrazení sledovat, že oba grafy mají svá optima (bod E - střed křivek nabídky a poptávky) v rozdílných kombinacích množství zákazníků a ceny. Prohnutí křivek v obou případech je zcela rozdílné, proto je nezbytné si uvědomit.

Lineární model

Lineární model budeme potkávat celý semestr. Připomeňte si co nejvíce o funkci: y = k.x + q.

Zakreslete různá zadání, popište, kde a jak se projevuje hodnota k, jak hodnota q. Najděte např. funkci IS nebo LM a určete, jaký má sklon, jaký posun, zakreslete ji do osových souřadnic, popište co nejpečlivě, co všechno jste si uvědomili.

Které ekonomické veličiny mohou způsobit posun některé z konkrétních ekonomických přímek (např. IS, LM, D, S aj.)? Zakreslete a popište.

Které ekonomické veličiny mohou způsobit otočení některé z konkrétních ekonomických přímek (např. IS, LM, D, S aj.)? Zakreslete a popište.

                                                                                                                                                                

Funkce se mění, roste nebo klesá. Je nutné si připomenou zobrazení funkcí na ose souřadnic. Navrhla jsem si čtyři funkce, u kterých je potřeba si uvědomit: jak se mění, odkud se mění a jak rychle se mění.

Funkce zobrazené v ose souřadnic nabývají klesajícího i rostoucího sklonu.
f: y = - x; se mění v hodnotě s rychlostí - 1 klesá, také f: y = 2 - x klesá rychlostí - 1 avšak mění se v hodnotě 2. Tyto dvě funkce jsou rovnoběžné.
f: y = 3x je rostoucí, mění se rychlostí 3 v hodnotě 0; současně f: y = 3x + 1 je rostoucí avšak od hodnoty 1 a s rychlostí 3, také jsou tyto dvě funkce rovnoběžné.



Funkce IS, posun, sklon:

Posun: vysoký agregátní výstup, ze kterého jsou tvořeny vysoké agregátní úspory, S>I - existuje nedostatečná investiční poptávka
Sklon: při nezměněné úrokové míře roste agregátní výstup (křivka se bude otáčet kolem bodu na ose y)

Úvod, Sklon funkce

Ekonomie je věda, zabývající se účelným lidským jednáním ve světě omezených zdrojů a neomezených potřeb.

Z hlediska zkoumání ekonomického chování a rozhodování jednotlivců, domácností, firem (podniků) či státu se ekonomie dělí na mikroekonomii (zabývá se ekonomickým chováním jednotlivých subjektů, tedy jednotlivců, domácností, firem a státu; zkoumá např.ceny statků a výrobních faktorů, vliv daní na podnik atd.) a makroekonomii (zkoumá ekonomiku jako celek (na úrovni ekonomických agregátů), zkoumá např. HDP a hospodářský růst, cenová hladina, inflaci, nezaměstnanost atd.).

1. Sklon funkce

Máme za sebou první přednášku a je potřeba splnit některé povinnosti.