POZOR!!! Sklony IS, LM pro konkrétní změny citlivostí

Procvičujte příklady ze skript (elektronický text v repository) kapitola IS-LM, ale volte své vlastní zadání, tj. jiná čásla než jsou ve skriptech a než jsme řešili ve cvičeních!

KAŽDÝ STUDENT ALESPOŇ JEDEN Z NÁSLEDUJÍCÍCH 5 PŘÍKLADŮ - vždy početně i graficky, pokaždé odvozením přes AD, resp. L, ale také přímo z rovnic IS, resp. LM):

Každý odevzdaný příklad musí mít 4 části - pro přehlednost označte A, B, C, D - navzájem musí souhlasit, tj. nikdo nemůže mít chybný výsledek :-):

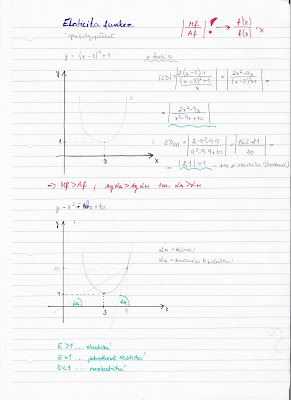
1. A Analytické odvození křivek z různými sklony + popis toho, co se stalo a čím to bylo zapřičiněno
2. B Grafické odvození křivek z různými sklony + popis toho, co se stalo a čím to bylo zapřičiněno + kontrola s předchozím
3. C Analytické vyjádření křivek s pouitím vzorců  + popis toho, co se stalo a čím to bylo zapřičiněno + kontrola s předchozím
4. D Grafické zakreslení výsledků z bodu C  + popis toho, co se stalo a čím to bylo zapřičiněno + kontrola s předchozím

Své příspěvky ve fórech TŘIĎTE do 4, resp. 5 skupin!

Řeště příklady s jinými čísly, než jsou ve skriptech nebo byla zvolena na cvičeních, tj. počítejte svůj příklad! ==> každý příklad bude jiný ( a od každého tam bude - aspoň jeden se 4 částmi :-) !)

1. úkol 2 ze skript: změna alfa (? sklon IS, multiplikační účinky) - volte změnu c
2. úkol 2 ze skript: změna alfa (? sklon IS, multiplikační účinky) - volte změnu t
3. úkol 3 ze skript: změna b (? sklon IS, multiplikační účinky)
4. úkol 5 ze skript: změna k (? sklon LM, multiplikační účinky)
5. úkol 5 ze skript: změna h (? sklon LM, multiplikační účinky)

Přehledně zapsat, přehledně zakreslit!!!

Nechť je četnost všech 4 příkladů srovnatelná, tj. dělej to, co je dosud ve fóru nejméně!

Sklony a posuny křivek IS, LM

Které veličiny ovlivní sklon, resp. posun křivky IS, resp. LM. Snažte se formulovat ekonomickou situaci, tu převeďte do mluvy lineárního modelu. Všechno kreslete, popisujte, zdůvodňujte. 

Modelovat můžete také polohy funkcí poptávky pro změny zafixování tzv. "cizích" veličin (AD pro různá i, resp. L pro různá Y).

Akumulace kapitálu

Jak jsem si procvičil akumulaci kapitálu. Zejména v obrázcích zdůrazněte vztah mezi derivací a určitým integrálem - všechno viz animovaný výklad (repository).

A početní příkladek: 

Makroekonomická rovnováha ve třísektorové ekonomice; multiplikační efekt (efekt změny autonomních výdajů, resp. mpc, resp. t)

Odvoďte multiplikační efekt ve tří sektorové ekonomice (případně s konkrétními čísly). Postupně můžete nejen "stavět nemocnici", ale také měnit velikost transferů, resp. autonomních daní, ba dokonce daňovou sazbu. Kdy se AD pouze posunuje, kdy se dokonce otáčí?

Multiplikační efekt vyznačte graficky.

DOPLNĚNÍ ÚKOLU (každý nechť má zápisky a hl. obrázky ke každé z těchto situací!): Analyzujte multiplikační efekty pro

1. změnu některých z autonomních výdajů (1-3 sektorová ekonomika)
2. změna mpc (zvýší se multiplikační efekt nebo sníží, proč?)
3. změna t (zvýší se multiplikační efekt nebo sníží, proč?)

Každou ze zakreslených situací si napište symbolicky (jako informaci, kterou stojí za to si zapamatovat), např. zvýšení mpc znamená strmější spotřební funkci, tzn. průsečíky pro rovnováhu jsou dále od sebe, tj. multiplikační efekt na důchod se pro větší mpc zesiluje - zapište v symbolech šipek, implikací atd.

Elasticita, včetně paradoxu velké úrody atd.

Příklady k postupnému procvičování

• Zvol funkci rostoucí, resp. klesající a urči graficky jejich elasticity (viz přednáškové slidy).
• Zvol funkci nabídky (kvadratickou) a urči její elasticitu jako funkci, pak v jednom bodě - početně, graficky (viz příklad ze cvičení).
• Skupinový příklad pro změny diskrétní (pro poslední dodatečnou jednotku, viz Vaše ekonomické příklady, např. o snižování cen letenek apod.) - jen pro zájemce (nemusíte).
• Paradox velké úrody, resp. snížení poplatků za telefon (velmi často bývá na písemkách)!!!

Fórum: vztah funkcí mezní a průměrné

Kreslete sady obrázků Mf a Af a žádejte po svých kolezích ve skupince í výběr správné odpovědi - viz přednáška (začněte někdo upřesněním zadání, jak jste jej slyšeli, např. komentováním svého zadání a správného řešení).

Který z obrázků je správně?

Vztah mezi veličinami průměrnými a mezními - zadání v ppt. prezentaci

Řešte úkol z přednášky. Začněte někdo tím, že připíšete zadání, jak jste jej dostali z prezentace na přednášce.




A já už pokračuji jen úkolem...

Pozn. v druhém grafu, při kreslení čáry špatně vyšel odhad a minimum průměrných nákladů neprotíná množství 6, jak by správně měly ve svém minimu! 

Maximalizace zisku

Výpočtem hledejte maximální zisk pomocí dvou metod:

1. MC = MR (ekonomické pravidlo)
2. Hledání extrému funkce (využití diferenciálního počtu)

a hledejte spojitosti obou výpočtů.

Zakreslete pod sebe 3 související grafy a do nich VŠECHNY RELEVANTNÍ ÚDAJE A SOUVISLOSTI (POPIŠTE CO NEJVÍCE):

1. TR, TC
2. MR, MC
3. zisk pi

Hledejte pro funkce:

• TR = 11 300 Q - 22Q²
• TC = 4 Q³ - 16 Q² + 140 Q + 1780

Pro nákresy určujte vrcholy, resp. konvexnost a konkávnost funkcí aj.

Hladká funkce

"Křivka ekonomická je hladká (v bodě, resp. v intervalu) tehdy a jen tehdy, má-li spojitou derivaci."  

Inspirace -  studijní materiál z Repository s názvem Hladká funkce. 

Příklad ze 4.cvičení: